数据结构基础fds 课程笔记

DataStructure 课程笔记 数据结构基础 fds

chap02 Algorithm Analysis

$T(N)=O(f(N))$ $T(N)\leq c f(N)$
$T(N)=\Omega(f(N))$ $T(N)\geq c f(N)$
$T(N)=\Theta(f(N))$ $T(N)= c f(N)$
$T(N)=o(f(N))$ $T(N)=O(f(N))$ and $T(N)\neq\Theta(f(N))$
  • $\log^kN=O(N)$: algorithm grows very slowly.

chap03 ADT-List

  • ADT 抽象数据类型

  • The cursor implementation is usually significantly faster because of the lack of memory management routines.

  • 链表：先放在前，后放在后

  • Add Two Polynomials

    • 多项式加法函数

  • Reverse Linked List

    • 单向链表转置

  • stack：后放在上

    • A Pop on an empty stack is an error in the stack ADT.

    • Push on a full stack is an implementation error but not an ADT error.

    1
    2
    3
    4
    5
    6
    7
    struct  StackRecord {
    	int Capacity ; /* size of stack */
    	int TopOfStack; /* the top pointer */
    	/* ++ for push, -- for pop, -1 for empty stack */
    	ElementType *Array; /* array for stack elements */
     } ;

  • The stack model must be well encapsulated（封装）

  • 表达式

infix 中序 $a+b*c-d/e$
prefix 前序
postfix 后序 $abc*+de/-$

  • 尾递归一定能变成循环

  • queue：两边开，先入先出，后入后出

    1
    2
    3
    4
    5
    6
    7
    struct  QueueRecord {
    	int Capacity ;   /* max size of queue */
    	int Front;  /* 队列头预制0，指向最老元素 */
    	int Rear;   /* 队列尾预制-1，指向最新元素 */
    	int Size;  /* Optional - the current size of queue */
    	ElementType *Array;    /* array for queue elements */
     } ;

  • 循环队列需要保留一个空位

  • Evaluate Postfix Expression

    • 后序表达式计算

  • Deque

    • 双向队列

  • Pop Sequence

    • 检查是否可以这样 pop

chap04 Binary Tree& Search Tree

4.1 Binary Tree

  • There are $N-1$ edges in a tree with $N$ nodes.
  • degree
    • of node: 有几个儿子
    • of tree: 树中拥有对多个儿子的节点的 degree
  • length of path: 一路上有多少条边
  • $Depth(root) = 0$
  • $Height(leaf) = 0$
  • 第$i$层最多有节点$2^{i-1}$个
  • 深度为$k$的树最多有节点$2^k-1$个
  • threaded binary trees 搜索二叉树，前序/中序/后续
    • 左指针指向遍历的前一个，右指针指向后一个

4.2 Search Tree

  • Binary Search Tree：左小右大，互不相同
  • Isomorphic
    • 树的对称
  • traversal
    • O(N)
    • 前序 preorder
    • 中序 inorder
    • 后序 postorder
    • 层级 level
  • ZigZagging on a Tree
  • Check BST
    • 判断是否为 BST
    • 返回层数 level
  • Binary Search Tree
    • 建立 BST
    • 判断两 BST 是否一样
  • 线索二叉树
    • 记 ptr 指向二叉链表中的一个结点，以下是建立线索的规则：
      （1）如果 ptr->lchild 为空，则存放指向中序遍历序列中该结点的前驱结点。这个结点称为 ptr 的中序前驱；
      （2）如果 ptr->rchild 为空，则存放指向中序遍历序列中该结点的后继结点。这个结点称为 ptr 的中序后继；

chap05 Priority Queues

  • 完全二叉树高为$h$, 节点数$2^h$到$2^{h+1}-1$

  • $h=\lfloor \log N\rfloor$

  • 最小堆/最大堆排序

    • 时间复杂度$\log_2 N$

  • d-heap

    • 每个节点有 d 个孩子
    • 时间复杂度$d\log_dN$
    • $i$的父亲$⌊(i+d−2)/d⌋$, 第一个儿子$ (i−1)d+2$, 最后一个儿子$ id+1$

  • Percolate Up and Down

  • Complete Binary Search Tree

    • 完全二叉搜索树建立
    • 树的前序遍历

chap06 Sort

img

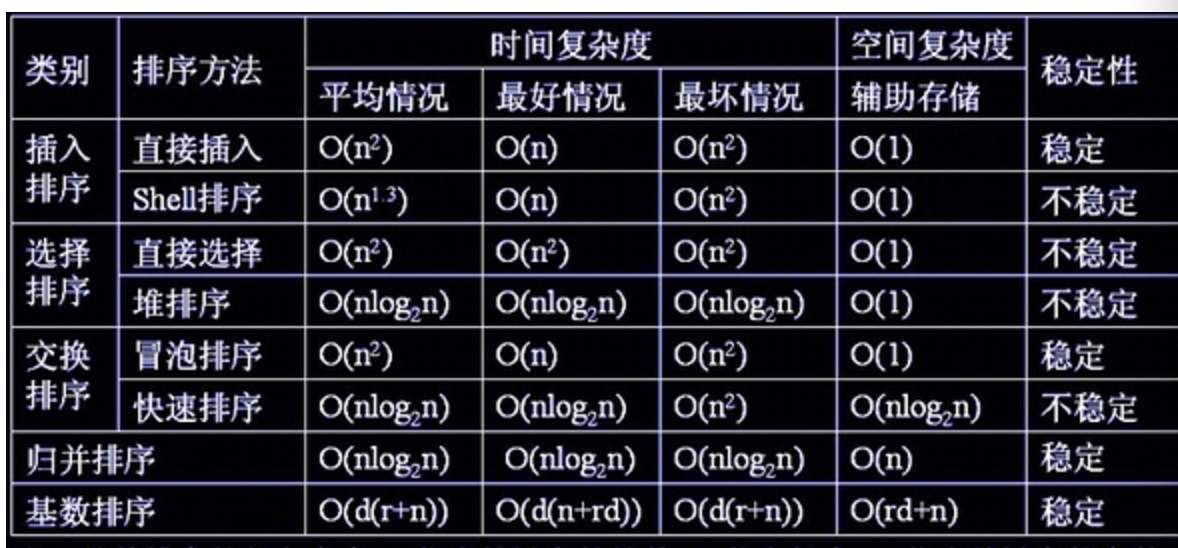
6.1 Shellsort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void Shellsort( ElementType A[ ], int N )
{
    int  i, j, Increment;
    ElementType  Tmp;
    for ( Increment = N / 2; Increment > 0; Increment /= 2 )
	/*h sequence */
	for ( i = Increment; i < N; i++ ) { /* insertion sort */
        Tmp = A[ i ];
	     for ( j = i; j >= Increment; j - = Increment )
             if( Tmp < A[ j - Increment ] )
                 A[ j ] = A[ j - Increment ];
        	else
		      break;
			A[ j ] = Tmp;
	} /* end for-I and for-Increment loops */
}

第一次间隔为$\lfloor N/2\rfloor$

后面每一次的间隔为前一次的一半

6.2 Heapsort

1
2
3
4
5
6
7
8
9
10
void Heapsort( ElementType A[ ], int N )
{  int i;
    for ( i = N / 2; i >= 0; i - - ) /* BuildHeap */
        PercDown( A, i, N );
    for ( i = N - 1; i > 0; i - - ) {
        Swap( &A[ 0 ], &A[ i ] ); /* DeleteMax */
        PercDown( A, 0, i );
    }
}

6.3 Mergesort

  • 需要额外线性空间
  • O( N + N log N )次归并
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void MSort( ElementType A[ ], ElementType TmpArray[ ],
		int Left, int Right )
{   int  Center;
    if ( Left < Right ) {  /* if there are elements to be sorted */
	Center = ( Left + Right ) / 2;
	MSort( A, TmpArray, Left, Center ); 	/* T( N / 2 ) */
	MSort( A, TmpArray, Center + 1, Right ); 	/* T( N / 2 ) */
	Merge( A, TmpArray, Left, Center + 1, Right );  /* O( N ) */
    }
}

void Mergesort( ElementType A[ ], int N )
{   ElementType  *TmpArray;  /* need O(N) extra space */
    TmpArray = malloc( N * sizeof( ElementType ) );
    if ( TmpArray != NULL ) {
	MSort( A, TmpArray, 0, N - 1 );
	free( TmpArray );
    }
    else  FatalError( "No space for tmp array!!!" );
}

  • Iterative Mergesort
    • 归并排序，每归并一次输出一次

6.4 Quiksort

  • 找一个基准，然后从右到左找一个比基准大的，从左到右找一个比基准小的，交换，一轮结束后，基准左边再做快排，右边也做快排
  • 数量少的时候插入排序更快

6.5 Tablesort

In the worst case there are $\lfloor N/2\rfloor $ cycles and requires $\lfloor 3N/2\rfloor$ record moves.

6.6 Bucketsort

  • 桶排序$O(N)$

    1. 通常桶越多，执行效率越快，即省时间，但是桶越多，空间消耗就越大，是一种通过空间换时间的方式

    2. 桶排序的时间代价，假设有m个桶，则每个桶的元素为n/m;

      当辅助函数为冒泡排序$O(n2)$时,桶排序为 $O(n)+mO((n/m)2)$;

      当辅助函数为快速排序时$O(nlgn)$时,桶排序为 $*O(n)+mO(n/m log(n/m))$

    3. 每个桶存储区间内的元素(区间为半开区间例如[0,10)或者[200,300) )

    4. 根据数据规模 n 划分，m 个相同大小的区间 （每个区间为一个桶，桶可理解为容器）

6.7 Insertionsort

  • inversion: pair ( i, j ) having the property that i < j but A[i] > A[j]

chap7 Hashing & Rehashing

  • Hashing collision: Two elements with different keys share the same hash value

chap8 Union-find

  • 不做优化的话最差时间复杂度是线性的

  • union by size/union by height

    • 用于如何合并两棵树的判断，小的成为大的的儿子/矮的成为高的的儿子
  • union by size
    • $S[root]=-size$
    • N 次插入 M 次搜索时间复杂度$O(N+M\log_2N)$
  • n 个元素 m 个关系，至少 n-m 个等价类
  • File Transfer
    • 寻找根
    • union by size
    • check 是否联通

chap9 Graph

9.1 Graph definition

  • $G(V,E)$

    • G: Graph
    • $V=V(G)$: 有限非空顶点集合
    • $E=E(G)$: 有限边集合
    • 不允许自成环

  • $G_1\subset G=V(G_1)\subset V(G)\&\&E(G_1)\subset E(G)$

  • connect graph：每个点到任一点都有通路

  • component of an undirected G: 最大连接子图

  • 强连通图

    有向图中，若任意两个顶点 Vi 和 Vj，满足从 Vi 到 Vj 以及从 Vj 到 Vi 都连通，也就是都含有至少一条通路，则称此有向图为强连通图。

  • 若有向图本身不是强连通图，但其包含的最大连通子图具有强连通图的性质，则称该子图为强连通分量

  • $degree(V)$顶点周围边的条数

    • n 顶点 e 边：$\sum_{i=0}^{n-1}degree(v_i)/2=e$

  • Adjacency Matrix 邻接矩阵

  • Adjacency List 邻接链表

9.2 Topological sort

  • AOV network: 有向不循环图
  • if a project is feasible, it must be irreflexive
    • irreflexive: 存在 i 到 j 有通路但无边
  • 拓扑排序不唯一
  • Is Topological Order
    • 拓扑排序的判断

9.3 Shortest path

  • If there is no negative-cost cycle, the shortest path from s to s is defined to be 0
  • $T = O( |V| + |E| )$
  • Shortest Path [3]
    • 最短路径条数+最短路径长度
  • Shortest Path [4]
    • 最短路径长度+最短路径上终点前的节点

9.4 Network flow

  • 最大流算法
    • 找当前节点上最大的路径
      • network.c dinic 算法
      • Universal Travel Sites

9.5 Minimum Spanning Tree

  • 边数=顶点数-1

9.6 MST

9.7 DFS

  • 欧拉回路

    • An Euler tour is possible if there are exactly two vertices having odd degree. One must start at one of the odd-degree vertices.
    • 欧拉通路、欧拉回路、欧拉图
      无向图：
      1. 设 G 是连通无向图，则称经过 G 的每条边一次并且仅一次的路径为欧拉通路；
      2. 如果欧拉通路是回路（起点和终点是同一个顶点），则称此回路为欧拉回路（Euler circuit）；
      3. 具有欧拉回路的无向图 G 称为欧拉图（Euler graph）。
        有向图：
      4. 设 D 是有向图，D 的基图连通，则称经过 D 的每条边一次并且仅一次的有向路径为有向欧拉通路；
      5. 如果有向欧拉通路是有向回路，则称此有向回路为有向欧拉回路（directed Euler circuit）；
      6. 具有有向欧拉回路的有向图 D 称为有向欧拉图（directed Euler graph）。
    1. 定理及推论
      欧拉通路和欧拉回路的判定是很简单的，请看下面的定理及推论。

    定理 5.1 无向图 G 存在欧拉通路的充要条件是：G 为连通图，并且 G 仅有两个奇度结点（度数为奇数的顶点）或者无奇度结点。

    推论 5.1：

    1. 当 G 是仅有两个奇度结点的连通图时，G 的欧拉通路必以此两个结点为端点。
    2. 当 G 是无奇度结点的连通图时，G 必有欧拉回路。
    3. G 为欧拉图（存在欧拉回路）的充分必要条件是 G 为无奇度结点的连通图。

    定理 5.2 有向图 D 存在欧拉通路的充要条件是：
    D 为有向图，D 的基图连通，并且所有顶点的出度与入度都相等；或者除两个顶点外，其余顶点的出度与入度都相等，而这两个顶点中一个顶点的出度与入度之差为 1，另一个顶点的出度
    与入度之差为-1。
    推论 5.2：

    1. 当 D 除出、入度之差为 1，-1 的两个顶点之外，其余顶点的出度与入度都相等时，D 的有向欧拉通路必以出、入度之差为 1 的顶点作为始点，以出、入度之差为-1 的顶点作为终点。
    2. 当 D 的所有顶点的出、入度都相等时，D 中存在有向欧拉回路。
    3. 有向图 D 为有向欧拉图的充分必要条件是 D 的基图为连通图，并且所有顶点的出、入度都相等。
    1. 欧拉回路的应用
      欧拉回路最著名的有三个应用，大家可以网上百度一下，这里不详述。
      哥尼斯堡七桥问题
      一笔画问题。
      旋转鼓轮的设计 4.欧拉回路的判定
      判断欧拉路是否存在的方法
      有向图：图连通，有一个顶点出度大入度 1，有一个顶点入度大出度 1，其余都是出度=入度。
      无向图：图连通，只有两个顶点是奇数度，其余都是偶数度的。
      判断欧拉回路是否存在的方法
      有向图：图连通，所有的顶点出度=入度。
      无向图：图连通，所有顶点都是偶数度。

  • Strongly Connected Components

    • 寻找回路：所有顶点的出、入度都相等时，D 中存在有向欧拉回路。
    1. 有向图 D 为有向欧拉图的充分必要条件是 D 的基图为连通图，并且所有顶点的出、入度都相等。
    2. 欧拉回路的应用
      欧拉回路最著名的有三个应用，大家可以网上百度一下，这里不详述。
      哥尼斯堡七桥问题
      一笔画问题。
      旋转鼓轮的设计
    3. 欧拉回路的判定
      判断欧拉路是否存在的方法
      有向图：图连通，有一个顶点出度大入度 1，有一个顶点入度大出度 1，其余都是出度=入度。
      无向图：图连通，只有两个顶点是奇数度，其余都是偶数度的。
      判断欧拉回路是否存在的方法
      有向图：图连通，所有的顶点出度=入度。
      无向图：图连通，所有顶点都是偶数度。

  • Strongly Connected Components

    • 寻找回路